kam

one of those blogs

Here is a question and an answer. They both propose a sequence of logical conclusions, but the answer is of course a “stronger” form of communicating this sequence:

Q: Do you create computer programs? Do you design them based on a business/problem domain? Do you understand this domain? Does this domain apply to the real world? Do you understand the real world? Do you create computer programs based on your understanding of the real world? Do you need to?

A: If you create computer programs they should be based on a business/problem domain. Hence you should understand this domain. Most of the problems/businesses are directly applicable/modeled after the real world. Hence you should understand the real world. Therefore you should create computer programs that apply/modeled after the real world (as much as possible, hence then you can “implement” the domain more closely / find a solution to a problem that can be directly applied to the real world).

While Q and A both follow the same logical sequence, I’d like to explore the Q of things. I’d like to question whether it is really true that we need to design/model our software/languages/libraries after the real world. And if it is true how close we need to “get the real world right” in our software design.

The first instinct, or my “natural intuitive power”, suggests that it is really the case. If we do model after the real world then we are building systems, evolving our metal and software friends who can potentially just coexist with us in our world following the laws of nature. Another supportive argument is a “business problem” that needs to be solved with software. For example “empowering businesses to predict nature”. Of course in order to predict something, we have to understand it and its environment. Currently we do that by taking petabytes of data and slapping it with something like Random Forest, and looking at probabilities… But what if our software just “knew” how things work, not based on historical data, but based on metaphysics, i.e. based on “what the world is and how it really works”.

While I am still not convinced we have to model our software after the real world “all the time”, I do lean towards this idea for the “most problems” I get to work with. In the least number of cases, for example when I get to write a stress test that sends billions of option quotes over the wire, I really don’t care whether it is an “ugly” imperative for loop or a “beautiful” pure function ‘send’ that is mapped over an immutable lazy sequence of quotes. This of course is an over simplification: firstly I should care, and it should be an imperative for loop, since it is faster, and secondly mapping functions over a sequence of things is not really a true modeling of a real world. Or is it?

If modeling after the real world is important, it is obvious we can’t omit “time” dimension when designing and creating software. But most of the time (no pun intended) we do just that. Most widely known/deployed software design approaches/patterns and instruments (e.g. programming languages) are stuck in “Wonderland“:

“Time has punished the Hatter by eternally standing still at 6 pm, and therefore there is always tea time”

Think about a C++/Ruby/Python/Java.. “object”. Does it have a notion of time? No. It may seem it has a notion of “now”, but when it is (its state) teared apart by multiple threads at the same time there is no notion of “now” anymore, and the poor object suffers terribly.

There is a classical talk by Rich Hickey “Are We There Yet?”, where he presents an “Epochal Time Model”:

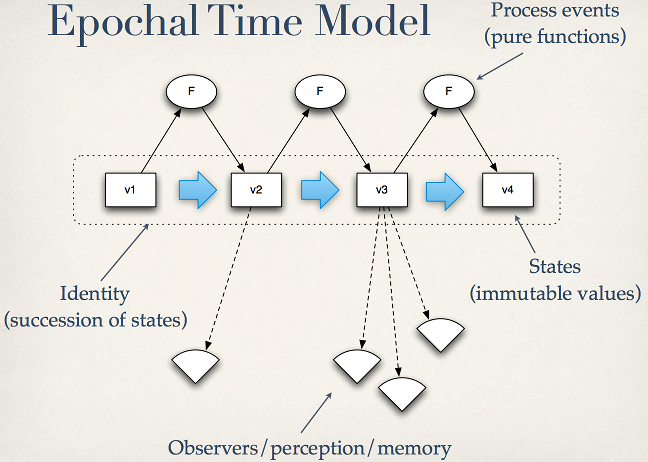
Where he introduces time as succession of states, and advocates immutability, i.e. the value of state “V1” is forever “V1” at that particular point in time. And we only get to state with a value “V2” after applying a function “F” to the state “V1”. Theoretically if we did support this notion of time, we could just talk to this “timeline”, which Rich calls an identity, and ask “what was its state at that point in time?” or more precisely “when/at which point in time was the state’s ‘value’ equal to “V1″?”. Practically we can do it with Datomic.

It’s more of a metaphysical thought, but if we are after true representation of the real world, does the “Epochal Time Model” really reflect how the world “changes”? If you wave your hand, does it just hyperjump from a state A to a state B? How granular is the path from A to B? Or is it absolutely “continuous” in which case there is no granularity, i.e. no smallest time interval? If you observe someone waving her hand, it is a different story: “the human eye and its brain interface, the human visual system, can process 10 to 12 separate images per second”, so here is a “state succession” interval. But what does really happen? Is the hand itself moving one planck at a time? Is it moving “de Broglie wavelength” at a time? Is it even important when modeling software?

Rich, and many other functional programming advocates, “sell” the idea of functional programming by stressing two things:

1. “This is how things work in the real world…”
2. “It is much easier to reason about…”

While the latter is mostly human based (how “we think”), it is connected to the #1. Since we think one way or another because our thinking is limited by what we know (+ imagination [this is controversial :]). And quite possibly our thinking is based on what we know “about the real world”, which we are part of.

It does seem to be important to model after the real world [ maybe :]. But why now? Why not 20 or 50 years ago? Did any of the programming languages actually aim to even connect to the real world before?

1957 Fortran: concepts included easier entry of equations into a computer

1958 Lisp: created as a practical mathematical notation for computer programs, influenced by the notation of Alonzo Church’s lambda calculus.

1958 ALGOL: was the standard method for algorithm description used by the ACM in textbooks and academic works

…

1962 Simula: created as a special purpose programming language for simulating discrete event systems

Ok, looks like the closest match is Simula that at least was created to simulate “something”. It is an ironic coincidence that it also is the source of Object Orientation (and actor model), but that is besides the point.

1971 Smalltalk-71 was created by Ingalls in a few mornings on a bet that a programming language based on the idea of message passing inspired by Simula could be implemented in “a page of code.”

1972 Prolog was motivated in part by the desire to reconcile the use of logic as a declarative knowledge representation language with the procedural representation of knowledge

1972 C was designed to be compiled using a relatively straightforward compiler, to provide low-level access to memory, to provide language constructs that map efficiently to machine instructions, and to require minimal run-time support.

1973 ML was conceived to develop proof tactics in the LCF theorem prover (whose language, pplambda, a combination of the first-order predicate calculus and the simply typed polymorphic lambda calculus, had ML as its metalanguage).

1975 Scheme started as an attempt to understand Carl Hewitt’s Actor model, for which purpose Steele and Sussman wrote a “tiny Lisp interpreter” using Maclisp and then “added mechanisms for creating actors and sending messages.”

1979 C++ remembering his Ph.D. experience, Stroustrup set out to enhance the C language with Simula-like features

1986 Erlang was designed with the aim of improving the development of telephony applications

1991 Java was originally designed (as “Oak”) for interactive television, but it was too advanced for the digital cable television industry at the time.

1995 JavaScript was originally implemented as part of web browsers so that client-side scripts could interact with the user, control the browser, communicate asynchronously, and alter the document content that was displayed

Looking at major languages created before “10/20 years ago”, their creational purpose does not seem to be “real world” related. For example the first two are clearly strictly math related.

So is it about Math? After all, we are “Computer Scientists” and although most of “Computer Programmers” are (unfortunately) very far from math, the science behind computers is very much based on it. Is the goal of mathematics, as a science, to model the real world? Let’s look how we “know to define” math:

math·e·mat·ics  [math-uh-mat-iks]
noun
1. The systematic treatment of magnitude, relationships between figures and forms, 
   and relations between quantities expressed symbolically.
2. A group of related sciences, including algebra, geometry, and calculus, 
   concerned with the study of number, quantity, shape, and space 
   and their interrelationships by using a specialized notation
3. Mathematical operations and processes involved in the solution of a problem 
   or study of some scientific field

Complimenting with “the current world intellect” (wikipedia):

Mathematics "has no generally accepted definition". 
Aristotle defined mathematics as "the science of quantity", 
Benjamin Peirce's "the science that draws necessary conclusions", 
                  "Mathematics is the mental activity which consists 
                  in carrying out constructs one after the other.",
Haskell Curry defined mathematics simply as "the science of formal systems", 
where a formal system is a set of symbols, or tokens, 
and some rules telling how the tokens may be combined into formulas.

From the above definitions it is hard to say whether the “real world modeling” is what Math is after, although we definitely know that Math is there to “explain” things in the world, oh.. wait, that’s Physics :]

If we are after modeling the real world (if it is indeed important), should we try to be as close as possible to the “reality”? Or should we just take the real world in by pieces and convenient definitions that suit a certain process, a problem at hand, programming style, hype, tech movement, etc.? It feels right to be close to the real world, since we are a part of it. It feels right to be close to ourselves. Are we just selfish? :]